To-sidet test

En matematiklærer ville undersøge hvilken metode der er bedst til at lære eleverne at dividere. Klassen, 4A blev undervist efter metode A og 4B  blev undervist efter metode B.

Efter undervisningsforløbet  fik hver klasse en prøve, der bestod af 50 simple regnestykker.  Der gives fra 0 - 50 point for en besvarelse.

• Kan der konstateres en signifikant forskel på gennemsnittene for de to prøver?

Alle elever på dette klassetrin er hele populationen, hvor vi ikke kender variansen. "Prøve A" og "Prøve B" er stikprøver, hvor variansen kan bestemmes.

Vi vil afgøre forskelligheden ved t-test. Der findes tre typer:

1. To stikprøver med ens varians
2. To stikprøver med forskellig varians
3. Parvis dobbelt stikprøve for middelværdi

• Hent og åbn projektmappen ErDerSignifikantForskelPaaGnsToStikpr.xlsx

Vi skal først teste om variansen i de to prøver er ens inden for et 95% signifikansniveau.

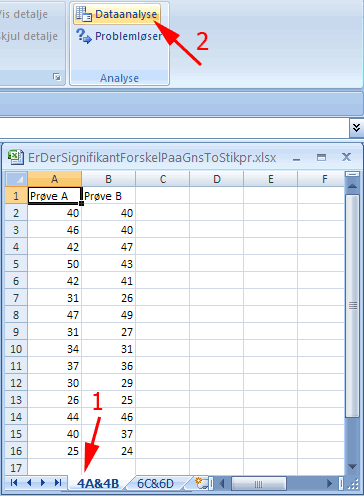
• Vælg fanen 4A&4B  nederst i projektmappen (1)

• Vælg  fanen  Data  | gruppen Analyse

• Tryk Dataanalyse (2)

Hvis dette værktøj ikke finde i din Excel, skal det installeres - se vejledning her: Installer Dataanalyse

Herved fremkommer boksen Dataanalyse.

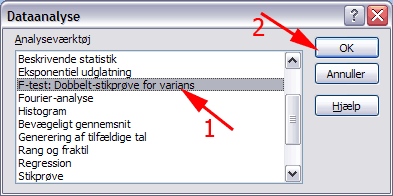
• Vælg F-test: Dobbelt-stikprøve for varians (1)

• Tryk OK (2)

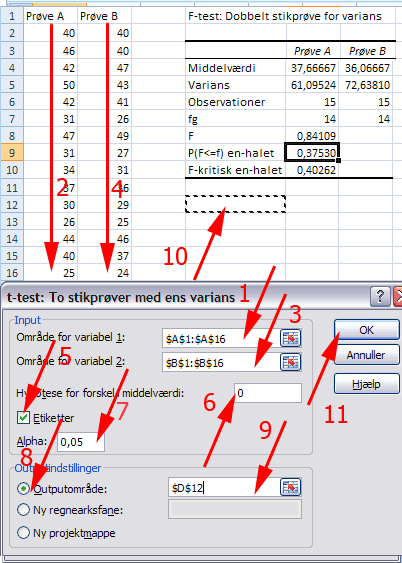
Herved fremkommer boksen F-test: Dobbelt-stikprøve for varians.

Vi vil teste nulhypotesen: Ingen forskel i varians

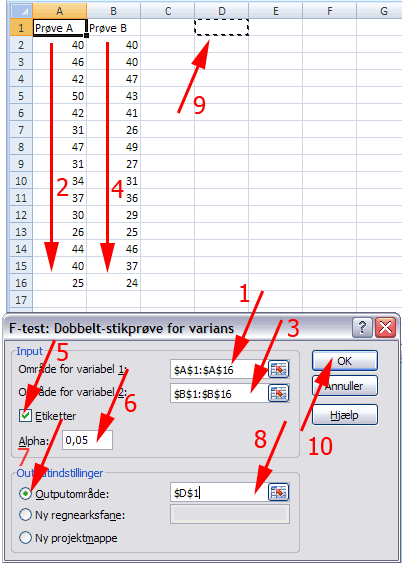
• Klik i øverste felt (1)

• Træk gennem celleområdet A1:A16 (2)

• Klik i næste felt (3)

• Træk gennem celleområdet B1:B16 (4)

• Afmærk Etiketter (5)

• Sæt Alpha = 0,05 (6)
  (Herved testes nulhypotesen på et 5% signifikansniveau)

• Afmærk Outputområde (7)

• Klik feltet ved Outputområde (8)

• Klik i Celle D1 (9)

• Tryk OK (10)

F er forholdet mellem de to varianser

P er sandsynligheden for nulhypotesen. P=38%. (1) Denne sandsynligheder er langt større end det valgte signifikansniveau på 5%.

Vi kan derfor konkludere, at der er statistisk belæg for at sige, at de to varianser ikke er forskellige (selv om de ser ret forskellige ud)

Vi skal derfor anvende T-test: To stikprøver med ens varians

• Vælg  igen fanen  Data  | gruppen Analyse

• Tryk Dataanalyse

Herved fremkommer boksen Dataanalyse.

• Vælg t-test: To stikprøver med ens varians (2)

• Tryk OK (3)

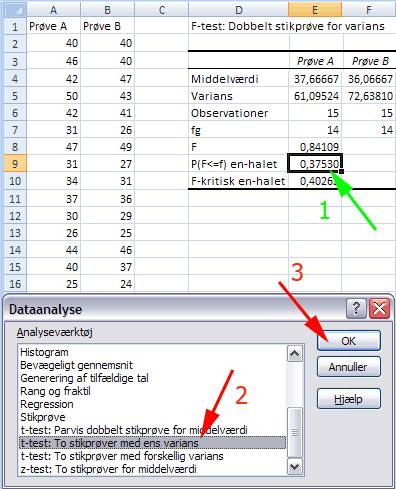
Herved fremkommer boksen t-test: To stikprøver med ens varians

Vi vil teste nulhypotesen: Ingen forskel i middelværdi

• Klik i øverste felt (1)

• Træk gennem celleområdet A1:A16 (2)

• Klik i næste felt (3)

• Træk gennem celleområdet B1:B16 (4)

• Afmærk Etiketter (5)

• Sæt Hypotese forskel i middelværdi = 0 (6)
  (Herved testes nulhypotesen)

• Sæt Alpha = 0,05 (7)
  (Herved testes nulhypotesen på et 5% signifikansniveau)

• Afmærk Outputområde (8)

• Klik feltet ved Outputområde (9)

• Klik i Celle D12 (10)

• Tryk OK (11)

fg er antal frihedsgrader = antal observationer - 1

Testværdien t-stat er forskellen i middelværdierne pr. standardfejl (den gennemsnitlige spredning).

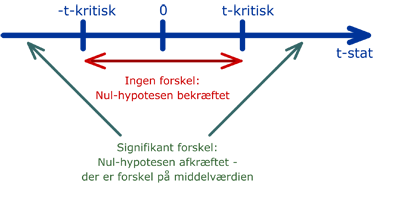
Hvis der skal kunne påvises en signifikant forskel i middelværdier skal den numeriske værdi af t-stat være større end t-kritisk.

Vi ser at t-stat = 0,54 < t-kritisk to-halet = 2,05

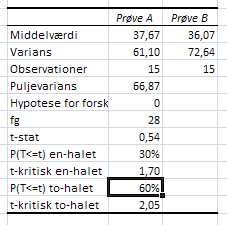
P er sandsynligheden for nulhypotesen.

Da vi ønsker at undersøge om der er forskel på middelværdierne skal vi her vælge at vurdere P(T<=t) to-halet, da t-stat både kan være større end  t-kritisk og mindre end -t-kritisk

P(T<=t) to-halet =60%.  Denne sandsynlighed er langt større end det valgte signifikansniveau på 5%.

Vi kan derfor konkludere, at der er statistisk belæg for at sige, at de to middelværdier ikke er forskellige (og de ser jo heller ikke ret forskellige ud)

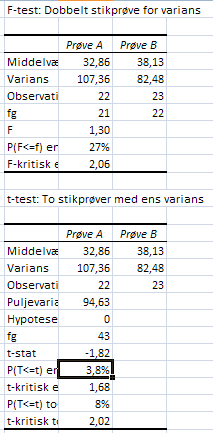
En-sidet test

Matematiklæreren i 6B havde en ide hans metode til at lære eleverne at løse ligninger var bedre end den traditionelle metode. Eleverne i 6A og 6B fik samme prøve

• Eleverne i 6B signifikant bedre til at løse ligninger end eleverne i 6A (En-sidet test)?

Nul-hypotesen er: 6B ikke bedre til at løse ligninger end eleverne i 6A

P(T<=t) en-halet =3,8%.  Denne sandsynligheder er mindre end det valgte signifikansniveau på 5%.

t- stat ligger uden for det kritiske interval.

Vi kan derfor konkludere, at der er statistisk belæg for at sige, at 6B er bedre til at løse ligninger end 6A inden for et signifikansniveau for nul-hypotesen på 5%.